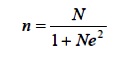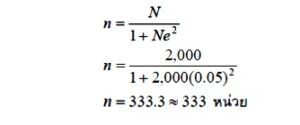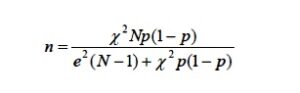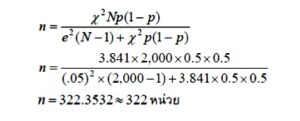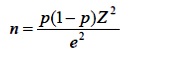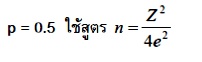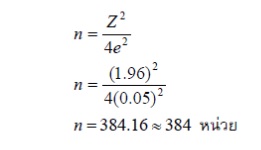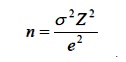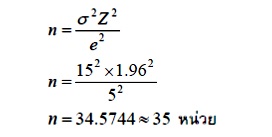การกำหนดขนาดกลุ่มตัวอย่าง (Sample Size)
เหตุผลสำคัญที่สุดของ การกำหนดขนาดกลุ่มตัวอย่าง เนื่องจาก การทำวิจัย หรือโครงการวิจัยประเภทอื่นๆ เช่น การทำดุษฎีนิพนธ์ การทำวิทยานิพนธ์ สารนิพนธ์ ค้นคว้าอิสระ ปัญหาพิเศษ ปริญญานิพนธ์ นักวิจัยจะประสบปัญหาเรื่องเวลา งบประมาณและทรัพยากรที่มีอย่างจำกัด ทำให้ไม่สามารถเก็บข้อมูลจากประชากรทั้งหมด ด้วยเหตุนี้การสุ่มตัวอย่างจากประชากรจึงมีความจำเป็น เพื่อให้เป็นตัวแทนของประชากรที่ต้องการศึกษา
ในโพสท์นี้ เราจะนำเสนอรายละเอียดสำคัญๆ เกี่ยวกับการกำหนดหรือการคำนวณขนาดกลุ่มตัวอย่าง โดยเฉพาะวิธีการที่ได้รับความนิยมใช้อย่างยาวนานเกินครึ่งศตวรรษอย่างสูตรของ Taro Yamane (1967) และวิธีการของ Krejcie & Morgan พร้อมทั้งเสนอข้อดี(จุดแข็ง) และข้อเสีย(จุดอ่อน) ของวิธีการกำหนดขนาดกลุ่มตัวอย่างของทั้งสองวิธีนี้ รวมถึงวิธีการคำนวณขนาดกลุ่มตัวอย่างอื่นๆ
ข้อควรรู้ ก่อนที่จะไปทำความรู้จักสูตร การกำหนดขนาดกลุ่มตัวอย่าง การเรียนรู้คำศัพท์เบื้องต้น ที่เกี่ยวข้องกับการหากลุ่มตัวอย่าง ได้แก่
- ประชากร (Population) คือ สมาชิกทุกหน่วยของสิ่งที่สนใจศึกษาวิจัย
- กลุ่มตัวอย่าง (Sample) คือ ส่วนหนึ่งของประชากร ที่นำมาเป็นตัวแทนของกลุ่มประชากรทั้งหมด จึงต้องมีการคัดเลือกกลุ่มตัวอย่างที่เหมาะสม เพื่อให้สามารถอ้างอิง ไปยังประชากรได้อย่างน่าเชื่อถือ
- การสุ่มตัวอย่าง (Sampling) คือ กระบวนการได้มาซึ่งกลุ่มตัวอย่าง ที่สามารถเป็นตัวแทนที่ดีของประชากรทั้งหมดได้

ขนาดของกลุ่มตัวอย่าง (Sample size) เป็นองค์ประกอบที่มีความสำคัญอย่างยิ่ง ต่อความน่าเชื่อถือของงานวิจัย เนื่องจากกลุ่มตัวอย่าง หรือ Sample Size คือ ตัวแทนที่ดีของประชากรที่ทำการศึกษา ด้วยเหตุนี้ ในแวดวงสถิติศาสตร์ จึงมีการพัฒนา และปรับปรุงวิธีการกำหนดขนาดกลุ่มตัวอย่างที่ถูกต้องและเหมาะสมมากที่สุด สำหรับงานวิจัย ซึ่งจนถึงปัจจุบันนี้ ยังเป็นที่ถกเถียงกันว่าวิธีการกำหนดหรือคำนวณขนาดกลุ่มตัวอย่างวิธีใดที่เหมาะสมที่สุด ทำให้มีการกำหนดขนาดกลุ่มตัวอย่างหลายวิธี เช่น การใช้สูตรการคำนวณ การใช้ตารางสำเร็จรูป และการกำหนดเกณฑ์ร้อยละของประชากรที่ศึกษา เป็นต้น โดยผู้วิจัยจะสามารถเลือกใช้ได้ตามความเหมาะสม
สำหรับ กลุ่มตัวอย่าง (Sample Group) หมายถึง บางส่วนของประชากร ที่ถูกเลือกสำหรับใช้เป็นตัวแทนของประชากรที่ทำการวิจัย การใช้กลุ่มตัวอย่าง ที่มีขนาดเล็กมากเกินไป ย่อมทำให้เกิดความคลาดเคลื่อนของการแปลผลการวิจัยได้มาก ในทางกลับกัน การใช้ขนาดกลุ่มตัวอย่างที่ใหญ่ จะมีโอกาสให้เกิดความคลาดเคลื่อนน้อย เพราะขนาดกลุ่มตัวอย่างที่มีขนาดใหญ่ ย่อมให้ข้อมูลที่มีความเที่ยงตรง สำหรับการคำนวณทางสถิติ ที่มีความถูกต้องมากกว่ากลุ่มตัวอย่างที่มีขนาดเล็ก กลุ่มตัวอย่าง ที่มีขนาดใหญ่มากเท่าใด ย่อมทำให้ค่าความคลาดเคลื่อน จากการสุ่มตัวอย่างจะน้อยลงมากเท่านั้น อย่างไรก็ตาม เมื่อถึง ณ จุดๆ หนึ่ง แม้ว่านักวิจัยจะทำการเพิ่มขนาดกลุ่มตัวอย่างให้มากขึ้นอีก แต่ความคลาดเคลื่อนจะไม่ลดลงตามมากนัก ((Kerlinger, 1972)
รูปแสดง ความสัมพันธ์ระหว่างค่าความคลาดเคลื่อนในการสุ่มตัวอย่าง กับ ขนาดของกลุ่มตัวอย่าง
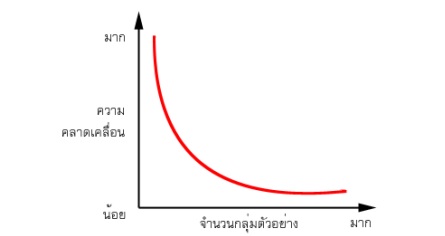
ที่มา : (Kerlinger, 1972)
ความจำเป็นที่ต้องมีการกำหนดขนาดกลุ่มตัวอย่าง
ขนาดกลุ่มตัวอย่างที่เหมาะสมสำหรับการวิจัย มีความสำคัญและมีความทจำเป็น ที่ผู้วิจัยจะต้องพิจารณาถึงปัจจัยต่างๆ หลายประการ เพื่อประเมินและเลือกใช้ในการเลือกขนาดกลุ่มตัวอย่าง ที่ถูกต้องและเหมาะสมกับงานวิจัยมากที่สุด (Librero, 1985) งานวิจัยจำนวนมากที่ขาดความน่าเชื่อถือ ทั้งที่องค์ประกอบส่วนใหญ่หรือเกือบทั้งหมดอยู่ในเกณฑ์ มาตรฐานทางวิชาการระดับสูง แต่มีการกำหนดขนาดกลุ่มตัวอย่างที่ไม่ถูกต้อง หรือไม่เหมาะสม ทำให้พลาดโอกาสในการตอบรับการตีพิมพ์ ในวารสารวิชาการ ที่ได้รับการยอมรับระดับสูงได้
- ค่าใช้จ่าย เวลา แรงงาน และเครื่องมือสำหรับใช้ในการเก็บรวบรวมข้อมูลจากกลุ่มตัวอย่างที่ใช้ ว่ามีเพียงพอที่จะทำได้หรือไม่ และใช้เวลามากเพียงใด
- ขนาดของประชากร หากประชากรมีขนาดใหญ่ ย่อมมีความจำเป็นที่จะต้องเลือกกลุ่มตัวอย่าง และหากประชากรมีขนาดเล็ก นักวิจัยอาจจะสามารถศึกษาได้จากประชากรทั้งหมดได้
- ความเหมือนกัน โดยหากประชากรมีความเหมือนกันมาก หรือมีความแตกต่างของลักษณะทางประชากรน้อย นั่นหมายถึงค่าความแปรปรวนในกลุ่มตัวอย่างย่อมมีขนาดน้อย นักวิจัยสามารถกำหนดขนาดกลุ่มตัวอย่างที่มีขนาดเล็กได้ ในทางกลับกัน หากประชากรมีลักษณะที่แตกต่างกันค่อนข้างมาก ค่าความแปรปรวนของประชากรภายในกลุ่มย่อมมีมากขึ้นตามไปด้วย จึงต้องใช้กลุ่มตัวอย่างที่มีขนาดใหญ่ เพื่อให้สามารถครอบคลุมคุณลักษณะต่างๆ ของประชากรที่ใช้ในการวิจัย
- ค่าความคลาดเคลื่อนของการสุ่มตัวอย่าง ในที่นี้ ค่าความคลาดเคลื่อนที่ยอมให้เกิดขึ้นได้จากการสุ่มตัวอย่างโดยปกติ จะยอมให้เกิดค่าความคลาดเคลื่อนได้ที่ระดับ 1% หรือ 5% (สัดส่วน 0.01 หรือ 0.05 ตามลำดับ) และยังขึ้นอยู่กับความสำคัญของเรื่องที่ทำการวิจัยด้วย หากเป็นเรื่องหรือการทำวิจัยที่มีความสำคัญมาก ควรจะให้เกิดความผิดพลาดน้อยที่สุด นักวิจัย จะกำหนดค่าความคลาดเคลื่อนที่ระดับ 1% เช่น งานวิจัยทางการแพทย์และทางวิศวกรรม เป็นต้น แต่หากเป็นงานวิจัยที่มีความสำคัญน้อยลงไป เช่น งานวิจัยที่สำรวจความพึงพอใจ หรือความต้องการสินค้าหรือบริการต่างๆ โดยทั่วไปจะกำหนดค่าความคลาดเคลื่อนที่ระดับ 5% เป็นต้น
- ค่าความเชื่อมั่น ผู้วิจัยควรกำหนดความเชื่อมั่น ว่ากลุ่มตัวอย่างที่สุ่มมานั้น มีโอกาสได้ค่าอ้างอิงไม่แตกต่าง จากค่าที่แท้จริงของประชากรประมาณเท่าใด เช่น หากกำหนดระดับความเชื่อมั่นที่ 95% หรือ ร้อยละ95 หมายถึง ค่าอ้างอิงมีโอกาสถูกต้อง 95% มีโอกาสผิดพลาด จากค่าที่แท้จริง 5% หรือร้อยละ 5 นั่นหมายถึงค่าที่ได้จากการสุ่มตัวอย่าง 95 กลุ่มจาก 100 กลุ่ม ที่สุ่มมาจากประชากรเดียวกัน จะไม่แตกต่างกันจากค่าที่แท้จริงของประชากร ซึ่งระดับความเชื่อมั่น อาจจะเพิ่มสูงขึ้น เป็นที่ระดับ 99% หรือลดลงเหลือ 90%
- ความถูกต้องแม่นยำ หากนักวิจัยต้องการความแม่นยำ ถูกต้อง และชัดเจนในเรื่องที่กำลังทำวิจัย จะต้องศึกษาวิจัยด้วยการใช้กลุ่มตัวอย่างที่มีขนาดใหญ่ กล่าวคือ กลุ่มตัวอย่างยิ่งมีขนาดใหญ่มากเท่าใด ผลการวิจัยจะยิ่งมีความแม่นยำมากขึ้นเท่านั้น
วิธีการกำหนดขนาดของกลุ่มตัวอย่าง
การกำหนดขนาดกลุ่มตัวอย่างมีด้วยกันหลากหลายวิธีด้วยกัน ในที่นี้จะเสนอการกำหนดขนาดของกลุ่มตัวอย่างจากการกำหนดเกณฑ์ การใช้สูตรคำนวณและการใช้ตารางสำเร็จรูป ซึ่งแต่ละวิธีสามารถอธิบายได้ต่อไปนี้
- การกำหนดเกณฑ์
ในกรณีนี้ผู้วิจัยต้องทราบจำนวนประชากรที่แน่นอนก่อนแล้ว ใช้เกณฑ์โดยกำหนดเป็นร้อยละของประชากรในการพิจารณาดังนี้ (ธีรวุฒิ เอกะกุล, 2543)
ถ้าขนาดประชากรเป็นหลักร้อย ควรใช้กลุ่มตัวอย่างอย่างน้อย 25%
ถ้าขนาดประชากรเป็นหลักพัน ควรใช้กลุ่มตัวอย่างอย่างน้อย 10%
ถ้าขนาดประชากรเป็นหลักหมื่น ควรใช้กลุ่มตัวอย่างอย่างน้อย 5%
ถ้าขนาดประชากรเป็นหลักแสน ควรใช้กลุ่มตัวอย่างอย่างน้อย 1%
- การใช้ตารางสำเร็จรูป
การกำหนดขนาดของกลุ่มตัวอย่างด้วยตารางสำเร็จรูป มีอยู่หลายประเภท ขึ้นอยู่กับ ความต้องการของผู้วิจัย ตารางสำเร็จรูปที่นิยมใช้กันในงานวิจัยเชิงสำรวจ ได้แก่ ตารางสำเร็จของทาโร ยามาเน่ และตารางสำเร็จรูปของเครจซี่และเมอร์แกน เป็นต้น
– ตารางสำเร็จของทาโร ยามาเน่
ตารางสำเร็จรูปของ ทาโร ยามาเน่ (Yamane, 1973 อ้างใน ธีรวุฒิ เอกะกุล, 2543) เป็นตารางที่ใช้หาขนาดของกลุ่มตัวอย่างเพื่อประมาณค่าสัดส่วนของประชากร โดยคาดว่าสัดส่วนของลักษณะที่สนใจในประชากร เท่ากับ 0.5 และระดับความเชื่อมั่น 95% ดังตารางที่ 1 วิธีการอ่านตารางผู้วิจัยจะต้องทราบขนาดของประชากร และกำหนดระดับความคลาดเคลื่อนที่ยอมรับได้ เช่น ต้องการหาขนาดของกลุ่มตัวอย่างจากประชากรที่มีขนาดเท่ากับ 2,000 คน ความคลาดเคลื่อนที่ผู้วิจัยยอมรับได้เท่ากับ 5% ขนาดของกลุ่มตัวอย่างที่ต้องการจะเท่ากับ 333 คน เป็นต้น
ตารางที่ 1 ขนาดของกลุ่มตัวอย่างของทาโร ยามาเน่ ที่ระดับความเชื่อมั่น 95 % และความคลาดเคลื่อนต่างๆ
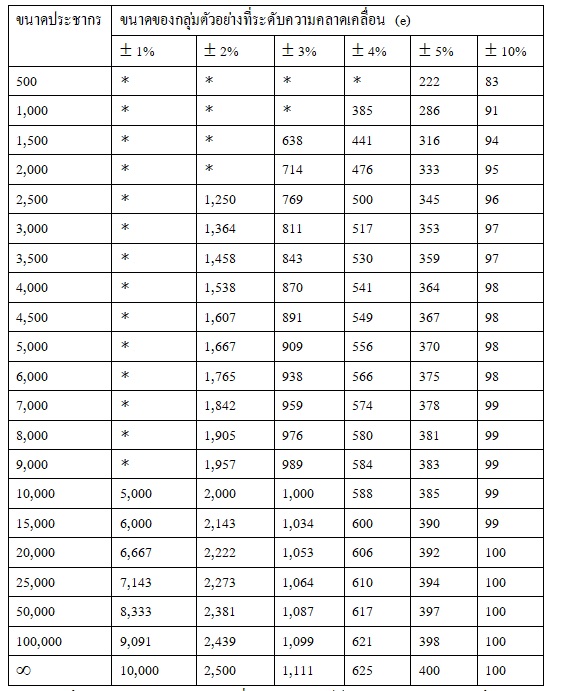
∗ หมายถึง ขนาดตัวอย่างไม่เหมาะสมที่จะ assume ให้เป็นการกระจายแบบปกติ จึงไม่สามารถใช้สูตรคำนวณขนาดของกลุ่มตัวอย่างได้
ที่มา : (Yamane, 1973 อ้างใน จักรกฤษณ์ สำราญใจ, 2544)
– ตารางสำเร็จรูปของเครจซี่และมอร์แกน
สำหรับตารางของเครจซี่และมอร์แกน (Krejcie & Morgan, 1970 อ้างใน ธีรวุฒิ เอกะกุล, 2543) ตารางนี้ใช้ในการประมาณค่าสัดส่วนของประชากรเช่นเดียวกัน และกำหนดให้สัดส่วนของลักษณะที่สนใจในประชากร เท่ากับ 0.5 ระดับความคลาดเคลื่อนที่ยอมรับได้ 5% และระดับความเชื่อมั่น 95% สามารถคำนวณหาขนาดของกลุ่มตัวอย่างกับประชากรที่มีขนาดเล็กได้ตั้งแต่ 10 ขึ้นไป ดังตารางที่ 2 วิธีการอ่านตารางผู้วิจัยต้องทราบขนาดของประชากร เช่น ถ้าประชากรมีขนาดเท่ากับ 2,000 คน ขนาดของกลุ่มตัวอย่างที่ต้องการจะเท่ากับ 322 คน เป็นต้น
ตารางที่ 2 ขนาดของกลุ่มตัวอย่างของเครซี่และมอร์แกน(ที่มา : Robert V. Krejcie and Earyle W. Morgan. 1970 อ้างใน ธีรวุฒิ เอกะกุล, 2543)

- การใช้สูตรคำนวณ
แม้การใช้ตารางกำหนดขนาดของกลุ่มตัวอย่างจะง่ายและสะดวกกับผู้วิจัย แต่บางครั้งผู้วิจัยอาจจำเป็นที่จะต้องคำนวณขนาดของกลุ่มตัวอย่างที่ขนาดประชากรหรือระดับความเชื่อมั่นอื่นๆที่แตกต่างออกไปจากตาราง ผู้วิจัยจำเป็นต้องการการคำนวณขนาดของกลุ่มตัวอย่างจากสูตรคำนวณ ซึ่งสูตรคำนวณขนาดของกลุ่มตัวอย่างมีหลากหลายวิธี ไม่ว่าจะเป็นสูตรของทาโร ยามาเน่ (Yamane, 1973) และสูตรของเครซี่และ มอร์แกน (Krejcie & Morgan, 1970) ทั้งสองสูตรนี้จำเป็นต้องทราบขนาดของประชากร แต่ถ้าไม่ทราบขนาดของประชากรก็อาจใช้สูตรของคอแครน (Cochran, 1977) รายละเอียดมีดังนี้
3.1 กรณีทราบขนาดของประชากร
3.1.1 สูตรของ ทาโร ยามาเน่ (Yamane, 1973 อ้างใน ธีรวุฒิ เอกะกุล, 2543)
n = ขนาดของกลุ่มตัวอย่างที่ต้องการ
N = ขนาดของประชากร
e = ความคลาดเคลื่อนของการสุ่มตัวอย่างที่ยอมรับได้
วิธีการคำนวณสูตรนี้ผู้วิจัยต้องทราบขนาดของประชากรที่ต้องการศึกษา (N) และกำหนดระดับความคลาดเคลื่อนที่ของการสุ่มตัวอย่างที่ยอมรับได้ (e) เช่น ถ้าประชากรที่ใช้ในการวิจัยมีจำนวน 2,000 หน่วย ยอมรับให้เกิดความคลาดเคลื่อนจากตัวอย่างได้ 5% ขนาดของกลุ่มตัวอย่างที่ต้องการเท่ากับ
3.1.2 สูตรของเครซี่และมอร์แกน
สูตรของเครซี่และมอร์แกน (Krejcie and Morgan, 1970 อ้างใน ธีรวุฒิ เอกะกุล, 2543) มีดังนี้
n = ขนาดของกลุ่มตัวอย่าง
N = ขนาดของประชากร
e = ระดับความคลาดเคลื่อนของการสุ่มตัวอย่างที่ยอมรับได้
χ2= ค่าไคสแควร์ที่ df เท่ากับ 1 และระดับความเชื่อมั่น 95% (χ2=3.841)
p = สัดส่วนของลักษณะที่สนใจในประชากร (ถ้าไม่ทราบให้กำหนด p = 0.5)
วิธีการคำนวณผู้วิจัยต้องทราบขนาดประชากรและสัดส่วนของลักษณะที่สนใจในประชากร และกำหนดระดับความคลาดเคลื่อนและระดับความเชื่อมั่นด้วย เช่น ถ้าประชากรที่ใช้ในการวิจัยมีจำนวน 2,000 หน่วย ยอมรับให้เกิดความคลาดเคลื่อนของการสุ่มตัวอย่างได้ 5% ที่ระดับความเชื่อมั่น 95% และสัดส่วนของลักษณะที่สนใจในประชากรเท่ากับ 0.5 ขนาดของกลุ่มตัวอย่างที่ต้องการเท่ากับ
3.2 ไม่ทราบขนาดของประชากร
3.2.1 สูตรของคอแครน (Cochran, 1977 อ้างใน ธีรวุฒิ เอกะกุล, 2543) ใช้ในกรณีที่ไม่ทราบขนาดของประชากรที่แน่นอน แต่ทราบว่ามีจำนวนมากและต้องการประมาณค่าสัดส่วนของประชากร มี 2 กรณีคือ
กรณีทราบค่าสัดส่วนของประชากร ใช้สูตร
และกรณีไม่ทราบค่าสัดส่วนของประชากร ใช้สูตร
n = ขนาดของกลุ่มตัวอย่างที่ต้องการ
p = สัดส่วนของลักษณะที่สนใจในประชากร
e = ระดับความคลาดเคลื่อนของการสุ่มตัวอย่างที่ยอมให้เกิดขึ้นได้
Z = ค่า Z ที่ระดับความเชื่อมั่นหรือระดับนัยสำคัญ
– ถ้าระดับความเชื่อมั่น 95% หรือระดับนัยสำคัญ 0.05 มีค่า Z = 1.96
– ถ้าระดับความเชื่อมั่น 99% หรือระดับนัยสำคัญ 0.01 มีค่า Z = 2.58
ตัวอย่างการคำนวณ เช่น ที่ระดับความเชื่อมั่น 95% ความคลาดเคลื่อนที่ยอมให้เกิดขึ้นได้ 5% และ สัดส่วนของลักษณะที่สนใจในประชากร เท่ากับ 0.5 ขนาดของประชากรที่ต้องการเท่ากับ
3.2.2 สูตรของคอแครน (Cochran, 1977 อ้างใน ธีรวุฒิ เอกะกุล, 2543)
สูตรนี้ใช้กรณีที่ไม่ทราบขนาดของประชากรที่แน่นอน และต้องการประมาณค่าเฉลี่ยของประชากร มีดังนี้
n = ขนาดของกลุ่มตัวอย่างที่ต้องการ
σ = ค่าส่วนเบี่ยงเบนมาตรฐานของตัวอย่าง
e = ความคลาดเคลื่อนของการสุ่มตัวอย่างที่ยอมให้เกิดขึ้นได้ (กรณีไม่ทราบ ค่า σ สามารถกำหนดค่า e เป็นเปอร์เซ็นต์ของσ เช่น 8% ของσ (e =0.08σ) หรือ 10% ของσ (e =0.10σ))
Z = ค่า Z ที่ระดับความเชื่อมั่นหรือระดับนัยสำคัญ
– ถ้าระดับความเชื่อมั่น 95% หรือระดับนัยสำคัญ 0.05 มีค่า Z = 1.96
– ถ้าระดับความเชื่อมั่น 99% หรือระดับนัยสำคัญ 0.01 มีค่า Z = 2.58
ตัวอย่างการคำนวณ เช่น ต้องการศึกษาคะแนนวิชาคณิตศาสตร์ ที่ระดับความเชื่อมั่น 95% ความคลาดเคลื่อนที่ยอมให้เกิดขึ้นได้ ± 5 คะแนน จากงานวิจัยที่ผ่านมาค่าเฉลี่ยเท่ากับ 70 คะแนน และ ค่าส่วนเบี่ยงเบนมาตรฐาน เท่ากับ 15 คะแนน ขนาดของกลุ่มตัวอย่างที่ต้องการ จะเท่ากับ
ขนาดของกลุ่มตัวอย่างเป็นสิ่งสำคัญของการศึกษาวิจัย ผู้วิจัยจะต้องได้ขนาดของกลุ่มตัวอย่างที่มีความเหมาะสม เป็นตัวแทนที่ดีของประชากรให้มากที่สุด ขนาดของกลุ่มตัวอย่างมีวิธีการหาได้ทั้งการเปรียบเทียบกับเกณฑ์ร้อยละของประชากร การใช้ตารางสำเร็จรูป และการใช้สูตรในการคำนวณ ผู้วิจัยจะเลือกใช้วิธีการใดขึ้นอยู่กับความต้องการของผู้วิจัย และความเหมาะสมของงานวิจัยแต่ละเรื่อง
เอกสารอ้างอิง
- 1. จักรกฤษณ์ สำราญใจ. (27 พฤศจิกายน 2544). การกำหนดขนาดของกลุ่มตัวอย่างเพื่อการวิจัย. สืบค้นวันที่ 25 ธันวาคม 2551, จาก http://www.jakkrit.lpru.ac.th/pdf/27_11_44/9.pdf
- 2. ธีรวุฒิ เอกะกุล. (2543). ระเบียบวิธีวิจัยทางพฤติกรรมศาสตร์และสังคมศาสตร์. อุบลราชธานี : สถาบันราชภัฎอุบลราชธานี.
- 3. พวงรัตน์ ทวีรัตน์. (2543). วิธีการวิจัยทางพฤติกรรมศาสตร์และสังคมศาสตร์ พิมพ์ครั้งที่ 8,กรุงเทพฯ: จุฬาลงกรณ์มหาวิทยาลัย.