การวิเคราะห์องค์ประกอบ Factor Analysis

แนวคิดพื้นฐาน ความรู้เกี่ยวกับ การวิเคราะห์องค์ประกอบ (Factor Analysis)

1. ความหมายของ การวิเคราะห์องค์ประกอบ

Factor analysis มีชื่อเรียกในภาษาไทย หลายคำ เช่น การวิเคราะห์องค์ประกอบ การวิเคราะห์ตัวประกอบ การวิเคราะห์องค์ประกอบ เป็นต้น สำหรับในการเขียนรายงานครั้งนี้จะใช้คำว่า การวิเคราะห์องค์ประกอบ ซึ่งมีผู้ให้ความหมายไว้หลายท่าน ดังนี้

เพชรน้อย สิงห์ช่างชัย (2549) ให้ความหมายคือ การวิเคราะห์องค์ประกอบเป็นเทคนิคทางสถิติ สาหรับวิเคราะห์ตัวแปรหลายตัว (Multivariate analysis techniques) ที่ออกแบบมาเพื่อช่วยให้นักวิจัยได้ใช้แสวงหาความรู้ความจริงดังกล่าว เช่น นักวิจัยสามารถใช้การวิเคราะห์องค์ประกอบเชิงสำรวจ (Exploratory Factor Analysis หรือ EFA) ในการพัฒนาทฤษฎี หรือนักวิจัยสามารถใช้การวิเคราะห์องค์ประกอบเชิงยืนยัน (Confirmatory Factor Analysis หรือ CFA) ในการทดสอบหรือยืนยันทฤษฎี

สรุปได้ว่า การวิเคราะห์องค์ประกอบ เป็นการวิเคราะห์หลายตัวแปรเทคนิคหนึ่งเพื่อการสรุปรายละเอียดของตัวแปรหลายตัว หรือเรียกว่าเป็นเทคนิคที่ใช้ในการลดจำนวนตัวแปรเทคนิคหนึ่งโดยการศึกษาถึงโครงสร้างความสัมพันธ์ของตัวแปร และสร้างตัวแปรใหม่เรียกว่า องค์ประกอบ โดยองค์ประกอบที่สร้างขึ้นจะเป็นการนาตัวแปรที่มีความสัมพันธ์กันหรือมีความร่วมกันสูงมารวมกันเป็นองค์ประกอบเดียวกัน ส่วนตัวแปรที่อยู่คนละองค์ประกอบมีความร่วมกันน้อย หรือไม่มีความสัมพันธ์กันเลย

นอกจากนี้  การวิเคราะห์องค์ประกอบ ยังมีลักษณะที่สำคัญดังต่อไปนี้

1. เป็นเทคนิคการวิเคราะห์ข้อมูลที่เป็นการรวมตัวแปรที่มีความสัมพันธ์กันไว้ในกลุ่ม หรือ ใน Factor เดียวกัน
2. ตัวแปรที่อยู่ในกลุ่มเดียวกัน จะมีความสัมพันธ์กันในระดับสูง
3. ความสัมพันธ์เป็นไปได้ทั้งความสัมพันธ์ทางบวกหรือในทิศทางเดียวกัน และ ความสัมพันธ์ทางลบ หรือ ในทิศทางตรงกันข้าม
4. ตัวแปรที่อยู่ในแต่ละกลุ่ม หรือ ในแต่ละ Factor จะไม่สัมพันธ์กัน หรือ สัมพันธ์กันในระดับต่ำ (น้อยมาก)
5. เป็นการวิเคราะห์หลายตัวแปร
6. การวิเคราะห์องค์ประกอบ สามารถใช้ลดขนาดข้อมูล ให้เหลือน้อยที่สุด (ลดคำถามในการวัดตัวแปรแฝงนั่นอง)
7. เป็นเทคนิคสำหรับการสร้างตัวแปรใหม่ โดยใช้ข้อมูลจาก Factor Score
8. การวิเคราะห์องค์ประกอบ สามารถแก้ไขปัญหาสหสัมพันธ์ของตัวแปรอิสระในระดับสูง หรือ ปัญหา Multicollinearity ในการวิเคราะห์สมการถดถอยเชิงซ้อนได้

2. ประเภทของเทคนิคการวิเคราะห์องค์ประกอบ

เทคนิคของการวิเคราะห์องค์ประกอบ แบ่งออกเป็น 2 ประเภทคือ

2.1 การวิเคราะห์องค์ประกอบเชิงสำรวจ (Exploratory Factor Analysis)

การวิเคราะห์องค์ประกอบเชิงสำรวจจะใช้ในกรณีที่ผู้ศึกษาไม่มีความรู้ หรือมีความรู้น้อยมากเกี่ยวกับโครงสร้างความสัมพันธ์ของตัวแปรเพื่อศึกษาโครงสร้างของตัวแปร และลดจำนวนตัวแปรที่มีอยู่เดิมให้มีการรวมกันได้ การวิเคราะห์องค์ประกอบเชิงสำรวจจะใช้ในกรณีที่ผู้ศึกษาไม่มีความรู้ หรือมีความรู้น้อยมากเกี่ยวกับโครงสร้างความสัมพันธ์ของตัวแปรเพื่อศึกษาโครงสร้างของตัวแปร และลดจำนวนตัวแปรที่มีอยู่เดิมให้มีการรวมกันได้

2.2การวิเคราะห์องค์ประกอบเชิงยืนยัน (Confirmatory Factor Analysis)   

การวิเคราะห์องค์ประกอบเชิงยืนยันจะใช้กรณีที่ผู้ศึกษาทราบโครงสร้างความสัมพันธ์ของตัวแปร หรือคาดว่าโครงสร้างความสัมพันธ์ของตัวแปรควรจะเป็นรูปแบบใด หรือคาดว่าตัวแปรใดบ้างที่มีความสัมพันธ์กันมากและควรอยู่ในองค์ประกอบเดียวกัน หรือคาดว่า มีตัวแปรใดที่ไม่มีความสัมพันธ์กัน ควรจะอยู่ต่างองค์ประกอบกัน หรือกล่าวได้ว่า ผู้ศึกษาทราบโครงสร้างความสัมพันธ์ของตัวแปร หรือคาดไว้ว่าโครงสร้างความสัมพันธ์ของตัวแปรเป็นอย่างไรและจะใช้เทคนิคการวิเคราะห์องค์ประกอบเชิงยืนยันมาตรวจสอบหรือยืนยันความสัมพันธ์ว่าเป็นอย่างที่คาดไว้หรือไม่ โดยการวิเคราะห์หาความตรงเชิงโครงสร้างนั่นเอง

ความแตกต่างที่สำคัญของ การวิเคราะห์องค์ประกอบเชิงสำรวจ (EFA) และ การวิเคราะห์องค์ประกอบเชิงยืนยัน (CFA)

EFA

1. ใช้สำรวจโครงสร้างข้อมูล (ไม่มีธงตั้งไว้ ไม่มีการล็อกผล)
2. ใช้สำหรับการกำหนดจำนวนองค์ประกอบ
3. สามารถตั้งชื่อ องค์ประกอบภายหลังได้
4. ในบางครั้ง เมื่อวิเคราะห์แล้วใช้ไม่ได้

CFA

1. ใช้แนวคิด ทฤษฎีนำ (มีธง)
2. ทดสอบทฤษฎีด้วยข้อมูลที่ทำการเก็บรวบรวม และวิเคราะห์ผลได้
3. ทดสอบคุณภาพเครื่องมือ (จำเป็น)
4. ถูกใช้เป็นแบบจำลอง หรือ โมเดล การวัดของ โมเดลสมการเชิงโครงสร้าง หรือ Structural Equation Mofel (SEM)

3.วัตถุประสงค์ของเทคนิค Factor Analysis

1)  เพื่อศึกษาว่าองค์ประกอบร่วมที่จะสามารถอธิบายความสัมพันธ์ร่วมกันระหว่าง

ตัวแปรต่าง ๆ โดยที่จำนวนองค์ประกอบร่วมที่หาได้จะมีจำนวนน้อยกว่าจำนวนตัวแปรนั้น จึงทำให้ทราบว่ามีองค์ประกอบร่วมอะไรบ้าง โมเดลนี้ เรียกว่า Exploratory Factor Analysis Model  : EFA

2)  เพื่อต้องการทดสอบสมมุติฐานเกี่ยวกับโครงสร้างขององค์ประกอบว่า องค์ประกอบแต่ละองค์ประกอบด้วยตัวแปรอะไรบ้าง และตัวแปรแต่ละตัวควรมีน้ำหนักหรืออัตราความสัมพันธ์กับองค์ประกอบมากน้อยเพียงใด ตรงกับที่คาดคะเนไว้หรือไม่ หรือสรุปได้ว่าเพื่อต้องการทดสอบว่าตัวประกอบอย่างนี้ตรงกับโมเดลหรือตรงกับทฤษฎีที่มีอยู่หรือไม่ โมเดลนี้เรียกว่า Confirmatory Factor Analysis Model: CFA ซึ่งเทคนิคของ Factor Analysis สามารถสรุปได้เป็นรูปแบบดังนี้

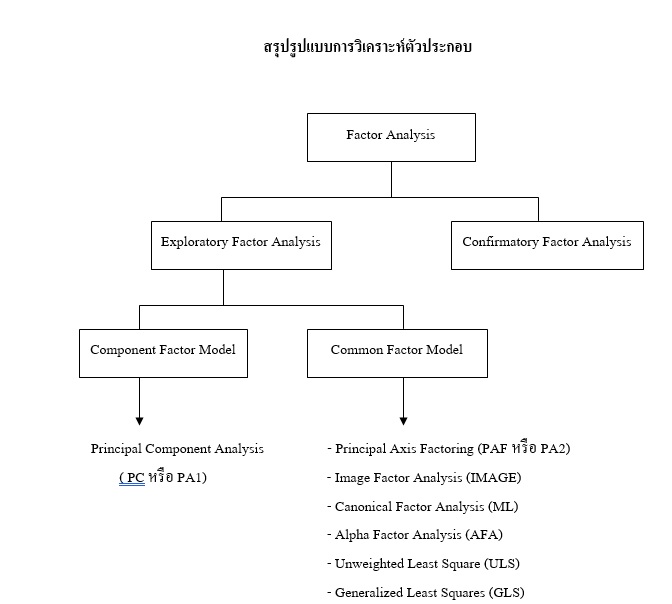
4.ประโยชน์ของเทคนิค Factor Analysis

1)  ลดจำนวนตัวแปร โดยการรวมตัวแปรหลาย ๆ ตัวให้อยู่ในองค์ประกอบเดียวกัน องค์ประกอบที่ได้ถือเป็นตัวแปรใหม่ ที่สามารถหาค่าข้อมูลขององค์ประกอบที่สร้างขึ้นได้ เรียกว่า Factor Score จึงสามารถนาองค์ประกอบดังกล่าวไปเป็นตัวแปรสาหรับการวิเคราะห์ทางสถิติต่อไป เช่น การวิเคราะห์ความถดถอยและสหสัมพันธ์ (Regression and Correlation Analysis) การวิเคราะห์ความแปรปรวน (ANOVA) การทดสอบสมมุติฐาน T – test Z – test และการวิเคราะห์จำแนกกลุ่ม (Discriminant Analysis) เป็นต้น

2)  ใช้ในการแก้ปัญหาอันเนื่องมาจากการที่ตัวแปรอิสระของเทคนิคการวิเคราะห์สมการความถดถอยมีความสัมพันธ์กัน (Multicollinearity) ซึ่งวิธีการอย่างหนึ่งในการแก้ปัญหานี้ คือ การรวมตัวแปรอิสระที่มีความสัมพันธ์ไว้ด้วยกัน โดยการสร้างเป็นตัวแปรใหม่หรือเรียกว่า องค์ประกอบ โดยใช้เทคนิค Factor Analysis แล้วนาองค์ประกอบดังกล่าวไปเป็นตัวแปรอิสระในการวิเคราะห์ความถดถอยต่อไป

3) ทำให้เห็นโครงสร้างความสัมพันธ์ของตัวแปรที่ศึกษา เนื่องจากเทคนิค Factor Analysis จะหาค่าสัมประสิทธิ์สหสัมพันธ์ (Correlation) ของตัวแปรทีละคู่ แล้วรวมตัวแปรที่สัมพันธ์กันมากไว้ในองค์ประกอบเดียวกัน จึงสามารถวิเคราะห์โครงสร้างที่แสดงความสัมพันธ์ของตัวแปรต่าง ๆ ที่อยู่ในองค์ประกอบเดียวกันได้ ทาให้สามารถอธิบายความหมายของแต่ละองค์ประกอบได้ ตามความหมายของตัวแปรต่าง ๆ ที่อยู่ในองค์ประกอบนั้น ทาให้สามารถนาไปใช้ในด้านการวางแผนได้ เช่น การพัฒนาพหุปัญญาสาหรับนักเรียนชั้นมัธยมศึกษาตอนต้นตามทฤษฎีพหุปัญญาของการ์ดเนอร์ (2546)

5.ข้อตกลงเบื้องต้นของการใช้สถิติการวิเคราะห์องค์ประกอบ

สถิติการวิเคราะห์องค์ประกอบ มีข้อตกลงเบื้องต้น (Stevens, 1992, 1996; Tabachnick & Fidell, 2001; Munro, 2001 : 309 อ้างใน เพชรน้อย สิงห์ช่างชัย, 2549)

1)  ตัวแปรที่คัดเลือกมาวิเคราะห์องค์ประกอบ ต้องเป็นตัวแปรที่มีค่าต่อเนื่อง หรือมีค่าในมาตราระดับช่วง (Interval scale) และมาตราอัตราส่วน (Ratio scale) เนื่องจากการวิเคราะห์องค์ประกอบ ตัวแปรที่คัดเลือกมาวิเคราะห์องค์ประกอบควรมีความสัมพันธ์ระหว่างตัวแปร

2) ตัวแปรที่คัดเลือกมาวิเคราะห์องค์ประกอบ ควรมีความสัมพันธ์ระหว่างตัวแปรในระดับสูง  (r = 0.30 – 0.70) รูปแบบความสัมพันธ์ระหว่างองค์ประกอบและตัวแปรที่อยู่ในรูปเชิงเส้น (linear) เท่านั้น

3) จำนวนตัวแปรที่คัดเลือกมาวิเคราะห์องค์ประกอบ ควรมีจำนวนมากกว่า 30 ตัวแปร

4) กลุ่มตัวอย่าง ควรมีขนาดใหญ่และควรมีมากกว่าจำนวนตัวแปร ซึ่งมักมีคาถามว่าควรมากกว่ากี่เท่า มีบางแนวคิดที่เสนอแนะให้ใช้จำนวนข้อมูลมากกว่าจำนวนตัวแปรอย่างน้อย 5 – 10 เท่า หรืออย่างน้อยที่สุด สัดส่วนจำนวนตัวอย่าง 3 ราย ต่อ 1 ตัวแปร

5) กรณีที่ใช้เทคนิคการวิเคราะห์องค์ประกอบหลัก (Principle component analysis)    ตัวแปรแต่ละตัวหรือข้อมูล ไม่จาเป็นต้องมีการแจกแจงแบบปกติ แต่ถ้าตัวแปรบางตัวมีการแจกแจงเบ้ค่อนข้างมาก และมีค่าต่ำสุด และค่าสูงสุดผิดปกติ (Outlier) ผลลัพธ์ที่ได้อาจจะไม่ถูกต้อง

6.ข้อจำกัดและปัญหาของการใช้สถิติการวิเคราะห์องค์ประกอบ

1.) ข้อจำกัดเรื่องจำนวนตัวอย่าง เนื่องจากการใช้สถิติการวิเคราะห์องค์ประกอบต้องใช้จำนวนตัวอย่าง (sample size) จำนวนมาก หากใช้ตัวอย่างน้อยค่าสัมประสิทธิ์สหสัมพันธ์จะต่ำ การประมาณจำนวนตัวอย่างที่ใช้ในการวิเคราะห์องค์ประกอบมีหลายแนวคิด

2) ปัญหาการวิเคราะห์องค์ประกอบมี 3 ประเด็น ดังนี้

2.1) การวิเคราะห์องค์ประกอบไม่มีตัวแปรตาม ซึ่งแตกต่างกับการทดสอบสถิติการวิเคราะห์ถดถอยเชิงพหุแบบปกติ สถิติการวิเคราะห์ถดถอยโลจิสติค สถิติการวิเคราะห์จาแนกประเภท  และการวิเคราะห์เส้นทาง ดังนั้น สถิติการวิเคราะห์องค์ประกอบ จึงไม่สามารถใช้แก้ปัญหาการวิจัยที่ต้องการหาตัวทำนายได้

2.2) ขั้นตอนการสกัดองค์ประกอบไม่สามารถระบุจำนวนรอบของการสกัดได้ ดังนั้นหลังจากขั้นตอนการสกัดองค์ประกอบนักวิจัยจึงไม่สามารถระบุจำนวนรอบของการสกัดองค์ประกอบได้ว่ามีกี่รอบจึงจะพอดี

2.3) ในปัจจุบันการวิจัยที่ต้องการทดสอบเพื่อลดจำนวนตัวแปร มีเพียงสถิติ

การวิเคราะห์องค์ประกอบเท่านั้น เนื่องจากสถิตินี้สามารถรวมตัวแปรหลาย ๆ ตัวให้อยู่ในองค์ประกอบเดียวกัน และทาให้เห็นโครงสร้างความสัมพันธ์ของตัวแปรที่ศึกษา โดยการหาค่าสัมประสิทธิ์สหสัมพันธ์ (Correlation) ของตัวแปรทีละคู่ แล้วรวมตัวแปรที่สัมพันธ์กันมากไว้ในองค์ประกอบเดียวกัน หลังจากนี้จึงสามารถวิเคราะห์ถึงโครงสร้างที่แสดงความสัมพันธ์ของตัวแปรต่าง ๆ ที่อยู่ในองค์ประกอบเดียวกันได้

ดังนั้นเมื่อนักวิจัยต้องการวิเคราะห์ให้ได้ผลการวิเคราะห์ดังกล่าวข้างต้น จึงมีสถิติให้เลือกใช้เฉพาะสถิติการวิเคราะห์องค์ประกอบเพียงตัวเดียว แต่ยังไม่มีวิธีการทางสถิติวิธีอื่น ๆ จึงทาให้นักวิจัยต้องเลือกใช้วิธีการวิเคราะห์องค์ประกอบทั้ง ๆ ที่วิธีนี้มีข้อจำกัดดังกล่าวข้างต้น

7.ขั้นตอนการวิเคราะห์องค์ประกอบ

ขั้นตอนการวิเคราะห์องค์ประกอบมีขั้นการทดสอบดังนี้

                    ขั้นที่ 1 กำหนดปัญหาการวิจัย ทบทวนองค์ประกอบตัวแปรจากทฤษฎี เก็บข้อมูล และเลือกวิธีวิเคราะห์องค์ประกอบตามวัตถุประสงค์การวิจัย

                   ขั้นตอนที่ 2  ตรวจสอบข้อมูลที่ใช้วิเคราะห์ว่าเป็นไปตามข้อตกลงหรือไม่ และสร้างเมทริกซ์ สหสัมพันธ์ (Correlation Matrix)

                   ขั้นที่ 3 สกัดองค์ประกอบ (Extraction Factor Analysis : Factor Extraction หรือ Initial Factors)

                   ขั้นตอนที่ 4 เลือกวิธีการหมุนแกน (Factors Rotation)

                   ขั้นที่ 5 เลือกค่าน้า หนักองค์ประกอบ (Factors Score)

                   ขั้นตอนที่ 6 ตั้งชื่อองค์ประกอบที่วิเคราะห์ได้

อ้างอิง

1. รับทำวิจัย
2. รับทำวิทยานิพนธ์
3. การเขียนบทคัดย่อ

Tag : การทำ is จ้างทำ is จ้างทำวิจัย จ้างทำวิทยานิพนธ์ จ้างทํางานวิจัย จ้างทําวิจัย ป.ตรี ราคา จ้างทําวิจัยราคา จ้างทําวิจัยราคาประหยัด จ้างทําวิจัย ราคาเท่าไหร่ จ้างทําวิทยานิพนธ์ จ้างทําวิทยานิพนธ์ราคา จ้างวิจัย ทําวิทยานิพนธ์ ทำงานวิจัย ทำงานวิทยานิพนธ์ บริการรับทำวิจัย รับจัดหน้าวิทยานิพนธ์ รับจ้างทำ is รับจ้างทํางานวิจัย ราคาถูก รับจ้างทํารายงาน รับจ้างทําวิทยานิพนธ์ รับจ้างทําวิทยานิพนธ์ ราคาถูก รับจ้างเขียนรายงาน รับทำ is รับทำ powerpoint รับทำ spss รับทำ thesis รับทำดุษฎีนิพนธ์ รับทำวิจัย รับทำวิจัยราคาถูก รับทำวิทยานิพนธ์ รับทำสารนิพนธ์ รับทำแบบสอบถาม รับทำโปรเจคจบ รับทํา thesis รับทํางานวิจัย รับทําปริญญานิพนธ์ รับทํารายงาน รับทําวิจัย ป.ตรี รับทําวิทยานิพนธ์ รับทําวิทยานิพนธ์ ป.โท รับทําวิทยานิพนธ์ ราคา รับทําวิทยานิพนธ์ราคาเท่าไหร่ รับทํา สารนิพนธ์ รับแปลงานวิจัย ราคารับทำวิทยานิพนธ์ วิจัย